Week 4

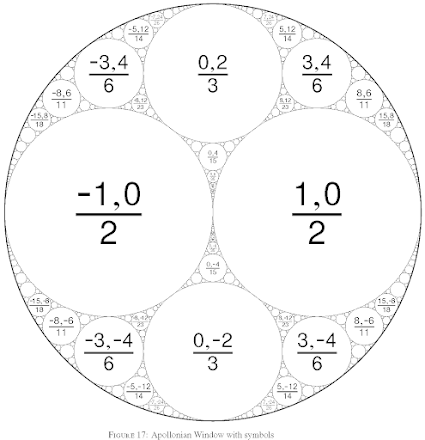
Inversions of disks are reflections in the Minkowski space!
$$\hbox{Ref}_{\mu(K)} \mu(D) \ = \ \mu\left( \hbox{Inv}_K \, D\right)$$

Simply:$$\hbox{Inv}_K \, D = D+2\langle K,D\rangle \, K$$ where $D$ is a disk (vector) and $K$ is a circle through which the disk is inverted.

Mini-challage:  Find the matrix representation of the inversion through $K$ and show it is a Lorentz transformation (belongs to $O(1,3)$).

A quick introduction to inversions in 2D (classical geometry).

Week 3

1. The crystalline structure of "apollohedron".

2. The homomorphism from the Euclidean group to Lorentz group, and their actions on the set of disks and the Minkowski space, respectively  $$\frac{\hbox{Eucl} (2)}{\mathcal D_2}  \quad \longrightarrow\quad \frac{\hbox{SO}(3,1)}{\mathbb M^{1,3}}$$  Just translations for now.

PS.  The above diagram is "approximate".  We shall extend it to the conformal group and take care of some details.  

[Click to enlarge]

Seminar: Week 2

A rain of implications  (Unbearable lightness of the derivations...)

1.  Conjugated disks :  $D + D' =2(A+B+C)$.
2.  (Generalized) Pappus' chains:  $C_{n+1}= 2C_n - C_{n-1} + 2(A+B)$.
3.  Pappus thread:  $K=\pm \frac{A-B}{2}$.
4.  Mid-circle:  $T= \pm \frac{A+B+C-D}{2}$.
5.  Points of tangency:  $P=\frac{A+B}{2}$. 
6.  Apollonian group.

Seminar: Week 1

1.  Introduction.  Plan for the near future.  Chart of the ideas (see below).

2.  The map $\mathcal D_2 \ \to \ \mathbb M^{1,3}$ that is central for this topic.