Temporary figures

 

Coxeter groups

17, 24, 31 October and 7 Nov

Devjani introduces us to the Coxeter groups and their representations.

See:
Video of Part 1  (17 Oct)
Video of Part 2  (24 Oct)

Video of Part 3  (31 Oct) 
Video of Part 4   (7 Nov)

Devjani strongly recommends Reflection Groups and Coxeter Groups by James E. Humphreys.  [Amazon]

2024 New series!

We are reviewing last year's material (see the previous posts). Once we finish, new posts will appear.  Below, we shall collect some new items from the current meetings.

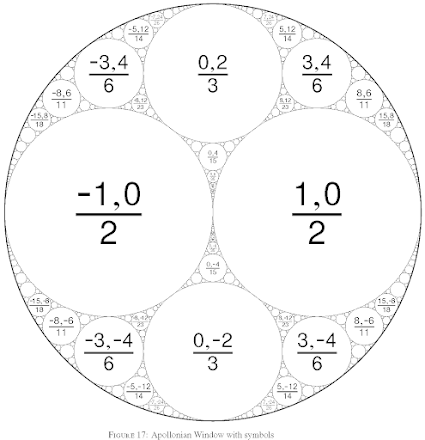
1.  Here are data to draw the Apollonian Window (or analyze the numbers). In the description in the sheet:

$x$ means $\dot x$,  $y = \dot y$, $b=\beta$, and $g=\gamma$

2.  The Pythagorean triples tree (pdf, 1 page)

BREAK!

Happy Holidays!

From 

bookbuilder.cast.org

Last few topics for the next semester

(1)  The $\hbox{SL}(2,\mathbb Z)$ tessellation of the uper half-plane $\mathbb C^{+}$, when viewed as a system of circles rather then tiles, and cosequently as vectors (points) in the Minkowski space, reveals a very simple algebraic algorithm for drawing it emerges, without tracing a group action!  The Dedekind tessellation (somewhat less known) is an effortless addition to this result.

(2)  "Superintegrality":  May every integral solution to Descartes' formula be a source of a geometric Apollonian disk packing such that all coordinates $(\dot x,\dot y, \beta,\gamma)$ and spinors be integral?  With the use of a certain "kaleidoscope group" this claim is confirmed. 

(3)  Depth function, defined on the set of all possible Descartes configurations, gives rise to an interesting fractal, and an interesting extension of group $\hbox{SL}(2,\mathbb Z)$ to a subgroup of  $\hbox{SL}(2,\mathbb Z[i])$.

(4)  Lens sequences: pleasant 4-term recurrence bilateral integer sequences (some of which may be observed in the Apollonian Window), accompanied with mysterious "underground" sequences that await geometric interpretation.

(5)  Plus other minor but interesting mathematical pieces (e.g., generalizations to higher dimensions).  Also, intriguing questions, unsolved problems, and possible projects.

WEEK 13

Integral packings, lattices, and Apollonian dust 

WEEK 12

1.  Descartes' Formula from the spinor theorems

2. Towards the integrality of Apollonian disk packing 

WEEK 11

Area of coronas and a Zeta funtion

$$A=\frac{\pi}{2}\; \sum_{\mathbf f\in \mathbb Z^2_o} \frac{1}{\left(\|\mathbf M\mathbf f \|^2 - B\right)^2}$$

where $\mathbf a$ and $\mathbf b$ are two adjacent spionors in a corona,  $\mathbf M= [\mathbf a|\mathbf b]$, and $B=\pm \,\mathbf a\times \mathbf b$.

The figure below shows spinors around the disk of curvature $B=23$ in the Apollonian Window.  Initial spins may be chosen $\mathbf a = [1,\, 5]$ and $\mathbf b = [3, -4]$. 

WEEK 10

Stern-Brocot tree and the magic quipu

Arrangements of spinors along a disk in an Apollonian packing has an interesting pattern...

WEEK 9

Can spinors be combed?...

We started with several simple reflections:

• The sum of the curvatures of two tangent disks is an Eulerian sum of squares due to the "Norm Theorem" (see the comix-like illustration from the previous meeting)
• Thm 6 = Thm 7  (visualized by continuous transformation) 
• If two adjacent spinors in an Apollonian disk packing are integral, so are all spinors in the packing.

 Then we defined "tuned spinors" and parallel transport of signs. 

WEEK 8

Seven principal theorems
(some serendipitous)
Proofs, proofs, proofs...

We reviewed the proofs of all basic theorems that reveal the secrets of tangency spinors.  They relate to the tangential arrangements of two, three, and four disks.  And they have the taste of "linearization" of the quadratic nature of the features ruling the curvatures,  much like Dirac equation is a linearization of the Klein-Gordon equation.  

The "comix" of the theorems is presented below.  One of the theorems may be viewed as the "square root of the Descartes Formula".

CHALLENGE:  Which is it? Can you derive the Descartes Formula from it?
Would squaring it be enough?...

[Click on to enlarge]

PS.  Is the following figure better?

WEEK 7

Descendance to the spinor spaces....

 

We proved the "curl u = 0" theorem.  Below is a selection of the "tangency spinors" in the Apollonian Window.  See this theorem at work.  Detect some other patterns... 

[Click on to enlarge]

WEEK 6

 A couple of "Apollonian gems":

1.  Pencils of lines and circles turn out to be points of intersection of 2D subspaces of $\mathbb M^{1,3}$ with the unit sphere (actually, hyperboloid).

2.  The Barning matrices that form a semigroup the orbit of which through [3,4,5] recovers all irreducible Pythagorean triples may be viewed as derived from certain three inversions in the Apollonian window.

Week 5

1.  Theorem (formula) for 4 disks in general configuration.

2.  Special case: Descartes' formula, and its extended version, both for tangent disks.

Define data matrix  $\mathbf D=[C_1|C_2|C_3|C_4]$  where $C_i = \begin{bmatrix}\dot x_i\\ \dot y_i\\ \beta_i\\ \gamma_i\end{bmatrix}$ 

Define the 4x4 configuration matrix $\mathbf F$ as a Gramian of inner products of pairs of disks: $$F_{ij} = \langle C_i , C_j \rangle$$  The general (matrix) formula is $$\boxed {\quad D\, f D^T \ = \ g \phantom{\Big|^2}\ }$$ where $f = F^{-1}$ (needs to be calculated from $F$ for a particular configuration), and $g=G^{-1}$, i.e., $$g = \begin{bmatrix} -1&\ 0&0&0\\ \ 0 & -1 &0&0\\ \ 0& \ 0&0 & 2 \\  \ 0&\ 0&2&0 \end{bmatrix}$$  Teaser: Draw four mutually perpendicular circles. 

Week 4

Inversions of disks are reflections in the Minkowski space!
$$\hbox{Ref}_{\mu(K)} \mu(D) \ = \ \mu\left( \hbox{Inv}_K \, D\right)$$

Simply:$$\hbox{Inv}_K \, D = D+2\langle K,D\rangle \, K$$ where $D$ is a disk (vector) and $K$ is a circle through which the disk is inverted.

Mini-challage:  Find the matrix representation of the inversion through $K$ and show it is a Lorentz transformation (belongs to $O(1,3)$).

A quick introduction to inversions in 2D (classical geometry).

Week 3

1. The crystalline structure of "apollohedron".

2. The homomorphism from the Euclidean group to Lorentz group, and their actions on the set of disks and the Minkowski space, respectively  $$\frac{\hbox{Eucl} (2)}{\mathcal D_2}  \quad \longrightarrow\quad \frac{\hbox{SO}(3,1)}{\mathbb M^{1,3}}$$  Just translations for now.

PS.  The above diagram is "approximate".  We shall extend it to the conformal group and take care of some details.  

[Click to enlarge]

Seminar: Week 2

A rain of implications  (Unbearable lightness of the derivations...)

1.  Conjugated disks :  $D + D' =2(A+B+C)$.
2.  (Generalized) Pappus' chains:  $C_{n+1}= 2C_n - C_{n-1} + 2(A+B)$.
3.  Pappus thread:  $K=\pm \frac{A-B}{2}$.
4.  Mid-circle:  $T= \pm \frac{A+B+C-D}{2}$.
5.  Points of tangency:  $P=\frac{A+B}{2}$. 
6.  Apollonian group.